Het geheim van de gulden snede

Voor het maken van een perfecte tekening moet je niet alleen de verhoudingen van de Mens van Vitruvius kennen, zoals we gisteren zagen, maar ook de gulden snede voor ogen houden. Deze gulden snede is een stukje eeuwenoude wiskunde. De gulden snede of divina proportia (goddelijke proportie) geeft de perfecte verhouding tussen lijnen aan.

Bij de gulden snede verhoudt het grootste van de twee delen zich tot het kleinste, zoals het gehele lijnstuk zich verhoudt tot het grootste. Geven we het grootste deel aan met a en het kleinste deel met b, dan is de verhouding van beide zo dat a:b = (a+b):a. De gulden snede wordt afgekort met de Griekse letter φ (phi) en is in getallen uitgedrukt ongeveer gelijk aan 1,618.

De gulden snede komt prachtig terug in de rij getallen die de wiskundige naamgenoot van Leonardo Da Vinci, Leonardo van Pisa, in 1202 optekende. Leonardo van Pisa, die meestal Fibonacci werd genoemd (naar figlio di Bonaccio, zoon van Bonaccio, goedzak, de bijnaam van Fibonacci’s vader), publiceerde in dat jaar zijn Liber Abaci (‘Het boek van de abacus’) over algebra en de Arabische cijfers. Hiermee introduceerde hij dit cijferstelsel in Europa.

In datzelfde boek publiceerde hij de zogenaamde Fibonacci-rij, waarin elk element van de rij de som van de twee voorgaande elementen vormt, beginnend met 0 en 1. De rij blijkt interessante eigenschappen en verbanden te bezitten met onder andere de gulden snede. Het eerste deel van de rij ziet er als volgt uit: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, …

De rij van Fibonacci zit vol met eigenaardigheden. Zo is elke optelsom van tien opeenvolgende getallen uit de reeks deelbaar door elf. Om de zestig getallen wordt het laatste cijfer herhaald.

Als je de quotiënten van twee opeenvolgende Fibonacci-getallen op een rij zet, zie je iets opmerkelijks: 1/1 = 1; 2/1 = 2; 3/2 = 1,5; 5/3 ≈ 1,667; 8/5 = 1,6; 13/8 = 1,625; 21/13 ≈ 1,615; 34/21 ≈ 1,619; 55/34 ≈ 1,618; 89/55 ≈ 1,618. Deze quotiënten naderen een vaste waarde. Hoe verder je komt in de rij van Fibonacci, hoe dichter het quotiënt van twee opvolgende getallen in de buurt komt van φ, het gulden-snede-getal.

Konijnenparen
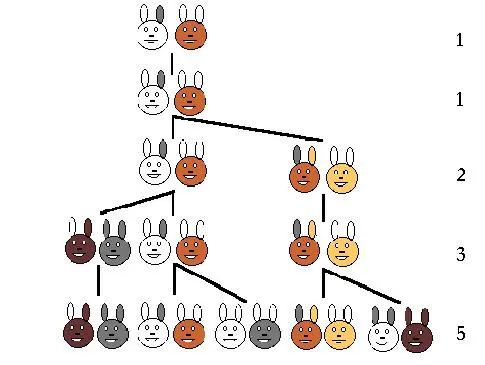
De rij van Fibonacci wordt vaak ook uitgelegd aan de hand van de groei van een konijnenpopulatie. Nu heb ik maar één konijn als huisdier, maar stel dat je twee konijnen (een mannetje en een vrouwtje) in een afgesloten hok zet. In de eerste maand heb je dus één paar. Na een maand zijn de konijnen volwassen en kan het vrouwtje jongen krijgen. De draagtijd is een maand. In de tweede maand heb je dus nog steeds één paar. Het vrouwtje krijgt een mannetje en een vrouwtje. In de derde maand heb je dus twee paren. Dat vrouwtje kan ook na een maand jongen krijgen. Er gaan geen konijnen dood en elk konijnenpaar krijgt elke maand een mannetje en een vrouwtje. Hoeveel konijnen heb je dan na een jaar? Precies; het aantal konijnenparen in een maand groeit dan precies volgens de Fibonacci-reeks: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ….

De gulden snede komen we elke dag tegen, vaak onbewust. De reeks is bijvoorbeeld aanwezig in een dennenappel, een schelp, in ons eigen lichaam en in de kunst. Waarom vind je bijvoorbeeld het ene schilderij mooier of beter dan een ander? Volgens de Italiaanse wiskundige Pacioli (1445-1517) komt dat vooral doordat de ene schilder de wetten van de wiskunde beter volgt en gehoorzaamt dan de ander. De verdeling van ruimtelijke vlakken op het doek ligt volgens Pacioli geheel en al vast in wiskundige verhoudingen, zoals de gulden snede. Hij ging zelfs zo ver dat hij de schilderkunst tot wiskundige figuren en vergelijkingen probeerde terug te brengen.

Dat biedt perspectief voor mij, want ik ben heel wat beter in wiskunde dan in het schetsen en schilderen… Wie de geheimen van Fibonacci wil doorgronden, moet ook even dit filmpje op Youtube kijken. Erg inspirerend!

Print dit artikel of sla het op als pdf